Eine Einführung in Soft-sensoren
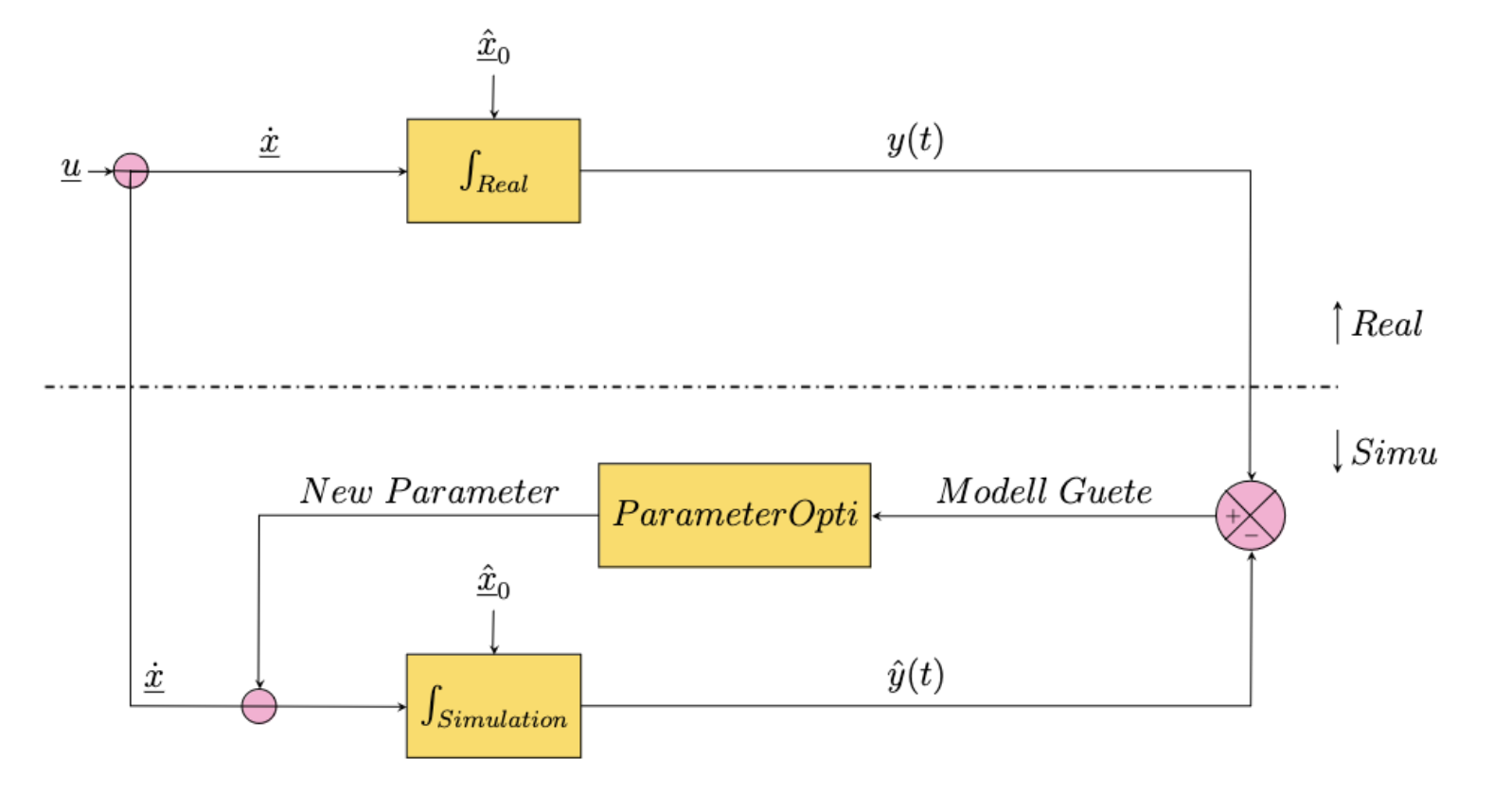
Ein Softsensor ist ein Software basierter Sensor. Er nutzt vorgegebene oder gemessene Eingänge und Ausgänge um, mithilfe der Zustandsgleichungen eines beliebigen Systems, die nicht messbaren Zustände zu schätzen und ggf. darzustellen (Knorn, 2021). Viele Zustände lassen sich nicht direkt oder nur schwer messen, daher ist die Verwendung von Softsensoren mit schnell verfügbaren Online-Daten sinnvoll. Die Beobachtung und Optimierung von Prozessen ist für die Forschung und Industrie wichtig. Ein Softsensor besteht grundsätzlich aus einem Modell und einer Korrektur. Das Modell sollte den Prozess vereinfacht abbilden und die Korrektur vergleicht dann die gemessenen Daten des realen Prozesses mit den vorhersagen des Modells. Somit können Softsensoren in Echtzeit schwer zu messende Größen ermitteln die Voraussagen für optimale Prozesseinflussnahme zulassen.
Modell
Systeme können vereinfacht von Modellen dargestellt werden, aus denen sich wiederum Schlussfolgerungen ziehen lassen. Die Wahl des Modells ist essenziell wichtig um bestimmte Aufgaben erfüllen zu können. Für biologische Modelle werden sehr häufig Differentialgleichungen (DGLs) für die Modelle benutzt, welche sich aus verschiedenen Kinetiken und und Massensowie Energie-Bilanzen ableiten. Sie leiten sich ab aus Gleichungen und Bilanzen mit denen sich Prozesse beschreiben lassen. Es werden DGLs auch deswegen benutzt, weil sich die Zustandsfunktionen nicht einfach ermitteln lassen, anders als ihre Ableitungen, der Änderung der Zustände über Bilanzen, die erstes ausdrücken können. Sie erlauben Vergleichbarkeit durch Reproduzierbarkeit der eingesetzten Parameter und Zustände. Daraus leitet sich ab, dass sie beinahe beliebige Erweiterbarkeit, Anpassbarkeit und Modifizierbarkeit erlauben.
Parameter
Parameter sind ein essenzieller Teil von DGL gestützten Modellen. Häufig lassen sich diese aus der Literatur erhalten, diese sind aber häufig nur Richtwerte. Mit einer Parameteridentifikation lassen sich theoretisch genaue Werte für die Parameter, mithilfe von Messdaten, erhalten. Wurden die Parameter eines Prozessen erhalten können sie mit einer geeigneten Zielsetzung optimiert werden.
Parameter-Identifikation
Die Parameteridentifikation nutzt eine Zielfunktion um dem Fit der Modellparameter an die Messdaten zu maximieren, bzw. ein Minimum der Funktion zu finden. Für nicht-lineare Systeme gibt es eine nicht-lineare Lösungsmethoden. Da biologische Systeme sehr häufig komplex sind und mit Komplexität häufig nicht-Linearität einhergeht, kommen dort nicht-lineare-Optimierungsalgorithmen, wie beispielsweise fmincon oder lsqnonlin zum Einsatz.